▶️선형검색
배열의 인덱스를 처음부터 끝까지 하나씩 증가시키면서 그 값이 속하는지 검사한다.
1
2
3
4
| n개의 원소가 있는 배열에서 50을 찾는다.
1) 0부터 n-1까지의 인덱스를 방문하여 값을 확인한다.
2) 원소가 50이면 true를 반환한다.
|
찾고자 하는 자료를 찾을 때까지 모든 자료를 확인해야 하기때문에 최악의 경우 리스트의 n개의 원소가 있을 때, n번 실행된다.
자료가 정렬되어 있지 않거나 정보가 없어 하나씩 찾아야 하는 경우에 유용하다.
▶️이진검색
배열이 정렬되어 있다면, 배열 중간 인덱스부터 시작하여 찾고자 하는 값과 비교하며 그보다 작은 인덱스 또는 큰 인덱스로 이동을 반복한다.
1
2
3
4
5
6
| n개의 원소가 있는 배열에서 50을 찾는다.
1) 원소가 없으면 false를 반환한다.
2) 중간 인덱스가 50이면 true를 반환한다.
3) 중간 인덱스가 50보다 크면 왼쪽을 검사한다.
4) 중간 인덱스가 50보다 작으면 오른쪽을 검사한다.
|
정렬되지 않은 리스트를 탐색하는 것보다 정렬한 뒤 탐색하는 것이 효율적이다.
▶️버블정렬
두 개의 인접한 자료값을 비교하면서 위치를 교환하는 방식으로 정렬하는 방법.
1
2
| 1.오름차순으로 정렬하기
6 3 8 5 2 7 4 1
|
1
2
| 2. 맨 앞의 6과 3의 위치를 교환
3 6 8 5 2 7 4 1
|
1
2
| 3. 그 다음 수인 6과 8은 pass, 8과 5의 위치를 교환
3 6 5 8 2 7 4 1
|
1
2
| 4. 반복하면 아래와 같이 정렬된다.
3 6 5 2 7 4 1 8
|
결과적으로 1 2 3 4 5 6 7 8 로 오름차순 정렬이 완성된다.
n개의 값이 주어졌을 때 각 루프는 각각 n-1번, n-2번 반복되므로 (n-1)*(n-2) = n^2-3n+2번의 교환이 필요하다. 정렬여부에 관계없이 비교를 해야하기 때문에 실행 시간의 상한과 하한이 같다.
▶️선택정렬
배열 안의 자료 중 가장 작은 수 (혹은 가장 큰 수)를 찾아 첫번째 위치(혹은 마지막 위치)의 수와 교환하는 방식으로 정렬하는 방법.
1
2
| 1. 오름차순으로 정렬하기
6 3 8 5 2 7 4 1
|
1
2
| 2. 가장 작은 값을 맨 앞 숫자와 교환
1 3 8 5 2 7 4 6
|
1
2
| 3. 1을 제외한 숫자 중 가장 작은 값을 두번째 숫자와 교환
1 2 8 5 3 7 4 6
|
더 이상 교환이 일어나지 않을 때까지 반복하면 오름차순 정렬이 완성된다.
▶️병합정렬
원소가 한 개가 될 때까지 계속해서 반으로 나누다가 다시 합쳐나가는 방식으로 정렬하는 방법.
재귀적으로 구현되기 때문에 재귀를 이해하면 더 쉽다.
1
2
| 1. 오름차순으로 정렬하기
7 4 5 2 6 3 8 1
|
1
2
| 2. 숫자들을 반으로 나눈다
7 4 5 2 | 6 3 8 1
|
1
2
| 3. 나눠진 부분 중 첫번째를 한번 더 반으로 나눈다
7 4 | 5 2 | 6 3 8 1
|
1
2
| 4. 한번 더 나눈다.
7 | 4 | 5 2 | 6 3 8 1
|
1
2
| 5. 원소가 한 개가 됐으므로 순서를 바꾸면서 병합한다
4 7 | 5 2 | 6 3 8 1
|
1
2
| 6. 다음 부분도 같은 방식으로 순서를 바꿔 병합한다
4 7 | 2 5 | 6 3 8 1
|
1
2
3
4
5
| 7.4 7 과 2 5 을 병합한다
각 부분의 숫자를 앞부터 순서대로 비교해 더 작은 숫자를 가져온다
4와 2를 비교해서 2를 가져온 후, 4와 5를 비교해 4를 가져온다
7과 5를 비교해서 5를 가져오고 남은 7을 가져온다
2 4 5 7 | 6 3 8 1
|
1
2
| 8. 이와 같이 뒷 부분의 6 3 8 1 도 나누고 순서를 바꿔 병합하는 과정을 거친다
2 4 5 7 | 1 3 6 8
|
1
2
| 9.마지막으로 각각 정렬된 왼쪽 4개와 오른쪽 4개를 병합한다.
1 2 3 4 5 6 7 8
|
숫자를 반으로 나누는 데 logn의 시간이 들고 반으로 나눈 각 부분들을 정렬하고 병합하는 데 n의 시간이 든다.
정렬여뷰에 관계없이 나누고 병합하는 과정이 필요하기 때문에 실행시간의 상한과 하한이 같다.
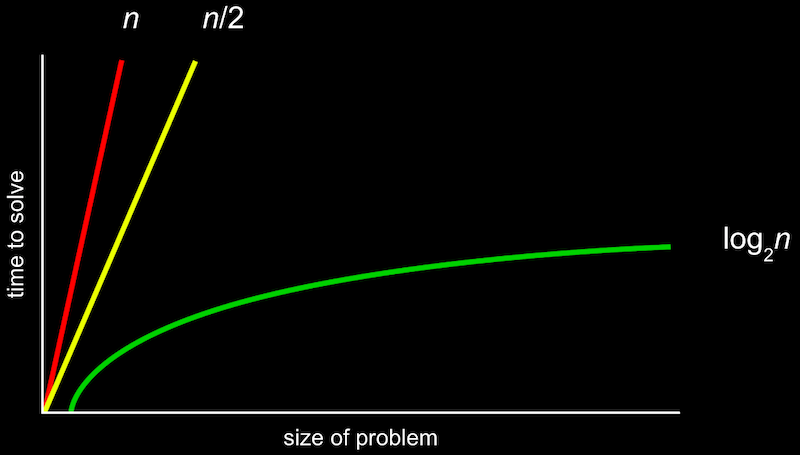
알고리즘을 실행하는 데 걸리는 시간
출처 : 네이버 부스트코스
Big O로 알고리즘 실행 시간의 상한을, Big Ω는 알고리즘 실행 시간의 하한을 나타낸다.
| 알고리즘 |
Big O |
Big Ω |
| 선형검색 |
O(n) |
Ω(1) |
| 이진검색 |
O(log n) |
Ω(1) |
| 버블정렬 |
O(n^2) |
Ω(n^2) |
| 선택정렬 |
O(n^2) |
Ω(n^2) |
| 병합정렬 |
O(nlogn) |
Ω(nlogn) |