이 포스팅은 kmooc의 인공지능을 위한 알고리즘과 자료구조 (성균관대학교 / 교수 허재필)를 듣고 정리했습니다.
비선형 자료구조
1. 트리
트리는 노드들의 집합체로 계층적인 관계를 나타낸다.
- 숫자나 이름등의 정보를 포함한다.
- 첫번째 노드인 루트 (root)가 존재한다.
- 하나의 노드는 다양한 개수의 자녀(children)을 가질 수 있다.
- 루트를 제외한 모든 노드는 하나의 노드를 부모(parent)로 가진다.
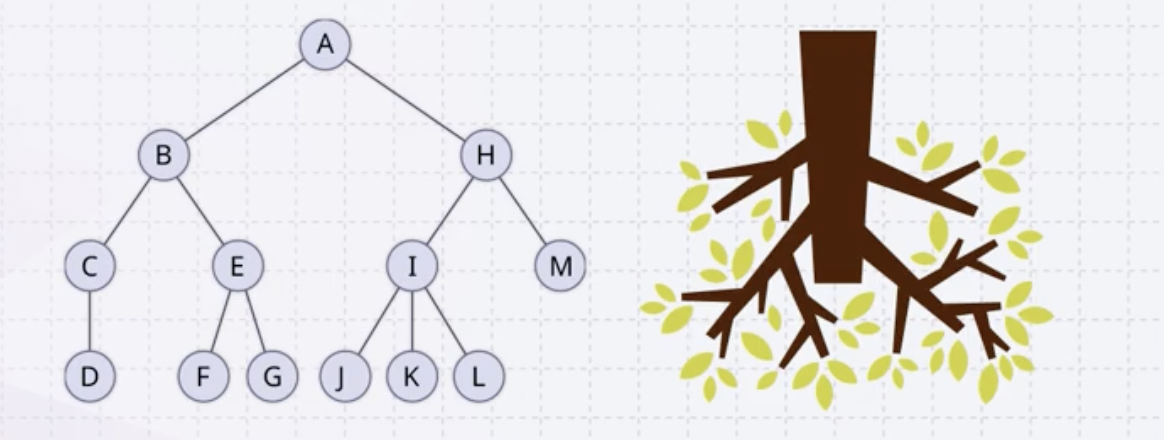
위의 그림에서 루트인 A는 B와 H를 자녀로 갖고 있다. 반대로 B는 A를 부모로 가진다.
컴퓨터 사이언스에서 말하는 트리는 실제 나무와 반대로 뿌리가 위에 있고 잎이 아래에 있는 형태를 보인다.
트리의 용어
- degree : 어떤 노드가 갖고 있는 자녀의 수
- sibling : 같은 노드를 부모로 갖는 노드들
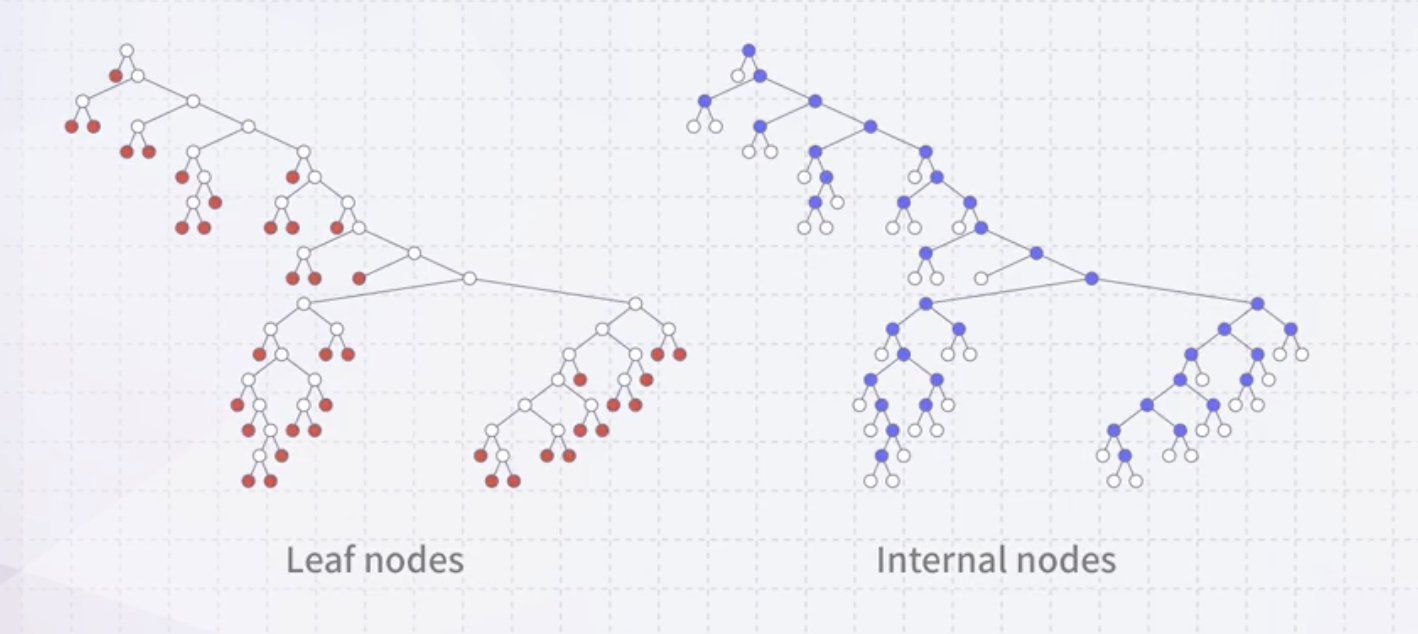
- Leaf node : 자녀가 없는(degree가 0인) 노드들
- Internal node : leaf node를 제외한 트리 내의 노드들
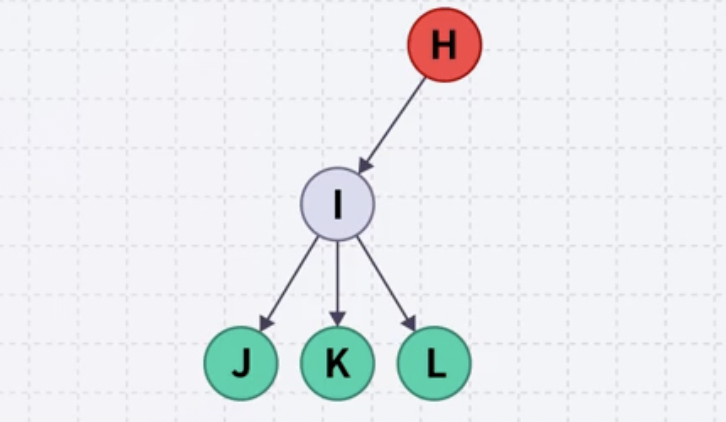예를 들어, 노드 I는 자녀가 J,K,L의 3개 이므로 degree가 3이다. 노드 J,K,L은 모두 노드 I를 부모로 가지므로 sibling이라고 할 수 있다.
( Unordered vs Ordered )
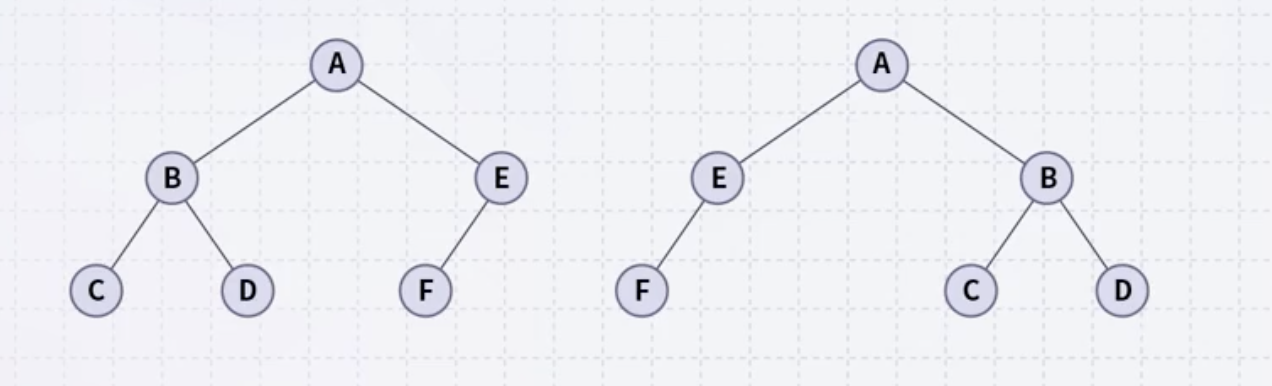A라는 루트 노드의 자녀 B와 E의 순서를 무시한다. 즉 위의 그림의 두 트리는 동일하다고 간주한다. 반대로 B와 E의 순서가 있다고 하면 두 트리가 다르다고 간주한다.
(Paths) 경로는 노드들의 시퀀스로 노드들의 순서를 나타낸다. 시퀀스에서 바로 앞의 노드가 그 다음 노드의 부모일때만 경로가 정의된다.
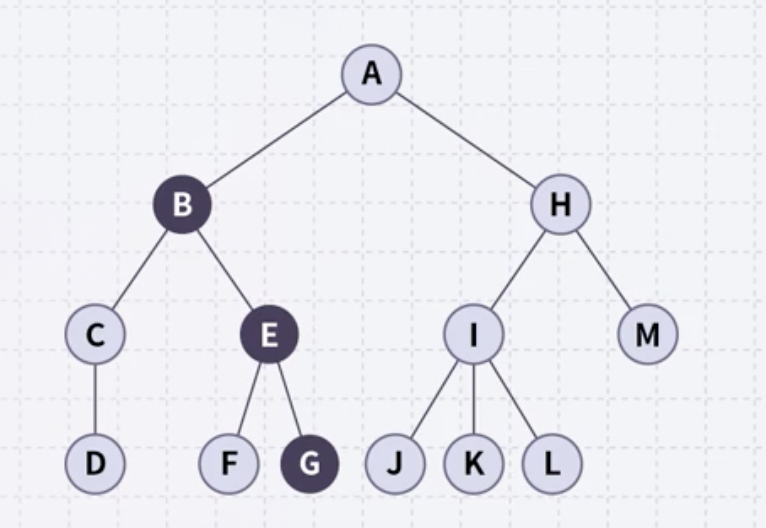
위의 트리에서 B-E-G로 이어지는 경로의 길이는 2이다. 경로에서 지나가는 선의 개수를 길이로 생각할 수 있다.
(Depth)
어떤 노드를 선택했을 때 루트노드로부터 이 노드로 이어지는 경로는 반드시 하나만 존재한다. 이 경로의 길이를 depth라고 한다.
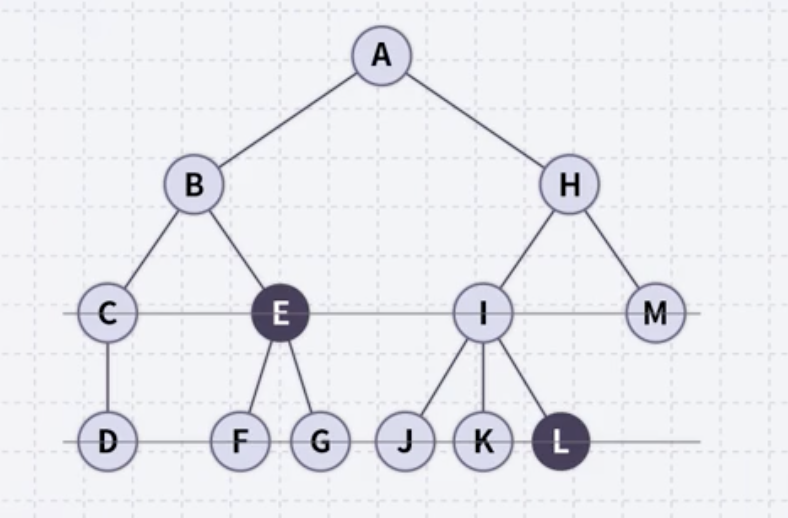예를 들어, 루트노드로부터 노드 K까지 가는 경로는 반드시 하나만 존재하고 이 경로의 depth를 3이라고 할 수 있다.
(Height) 트리의 모든 노드 중 depth가 가장 큰 값을 height라고 한다. 트리가 루트노드만 존재한다면 이 트리의 depth는 0이므로 height도 0이라고 할 수 있다. 정의에 따라서, 아무 노드도 없는 텅 빈 트리의 height는 -1이라고 표현한다.
(ancestor, descendant) 노드 a에서 노드 b로 이어지는 경로가 존재한다고 가정했을 때,
- a는 b의 ancestor(조상)이 되고
- b는 a의 descendant(자손)이 된다.
일반적으로, 자기자신을 포함해서 말한다.
루트 노드는 트리 내의 모든 노드의 조상이다.
2. 그래프
그래프는 어떤 데이터 사이의 인접한 정보를 저장하는 자료구조이다. 그래프에는 object와 relationship이 존재한다.
- object : 저장하고자 하는 객체. 예를 들어 오브젝트는 어떤 사람이나 도시가 될 수 있다. 오브젝트를 표현하는 노드를 vertex라고 한다.
- relationship : object사이의 관계성 (edge)
Undirected Graphs 방향이 없는 그래프
N개의 vertex가 있다고 했을 때, v1부터 vN까지의 N개의 vertex가 있고 이들을 연결하는 edge가 순서가 없는 pair로 이루어진다. 연결성을 표현하기 위해 adjacency matrix나 adjacency list를 쓸 수 있다.
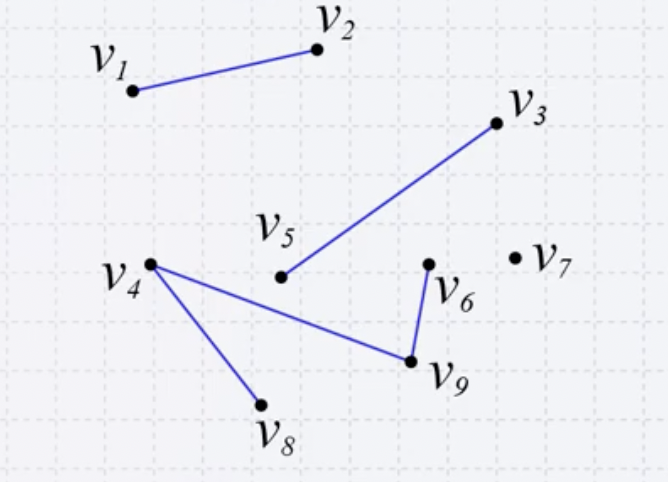
예를 들어, 위의 그림처럼 9개의 vertex가 있다고 하면 다섯개의 엣지가 존재한다.
E = ((v1,v2),(v3,v5),(v4,v8),(v4,v9),(v6,v9))
방향이 없기 때문에 {v1,v2}는 v1에서 v2로 가는 엣지, v2에서 v1으로 가는 엣지 모두 존재한다고 가정한다.
자기자신에서 자기자신으로 가는 엣지가 없다고 가정했을 때, V개의 vertex가 있는 undirected 그래프에서 엣지의 최대 갯수는 조합을 이용해 vC2로 표현할 수 있다.
(Degree) 트리와 마찬가지로 이웃 개수를 degree로 정의한다. 어떤 점을 기준으로 연결되어있는, 하나의 엣지로 갈 수 있는 vertex를 이웃이라고 한다.
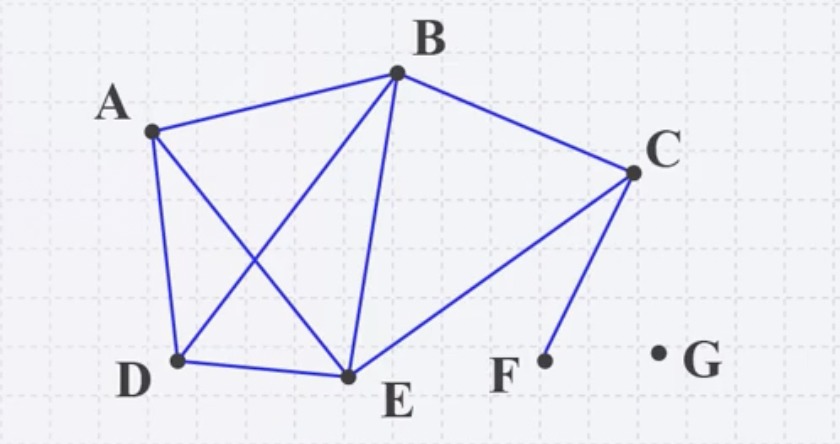
A의 degree는 3, F의 degree는 1, G의 degree는 0이라고 할 수 있다.
Sub-graphs 오리지널 그래프에서 엣지와 vertex를 추출한 것으로 서브그래프에 존재하는 모든 vertex와 엣지는 오리지널 그래프에 존재한다고 할 수 있다.
(Paths) 트리와 마찬가지로 노드의 시퀀스를 경로로 표현하며 경로의 길이는 몇 개의 엣지를 거치는가가 된다.
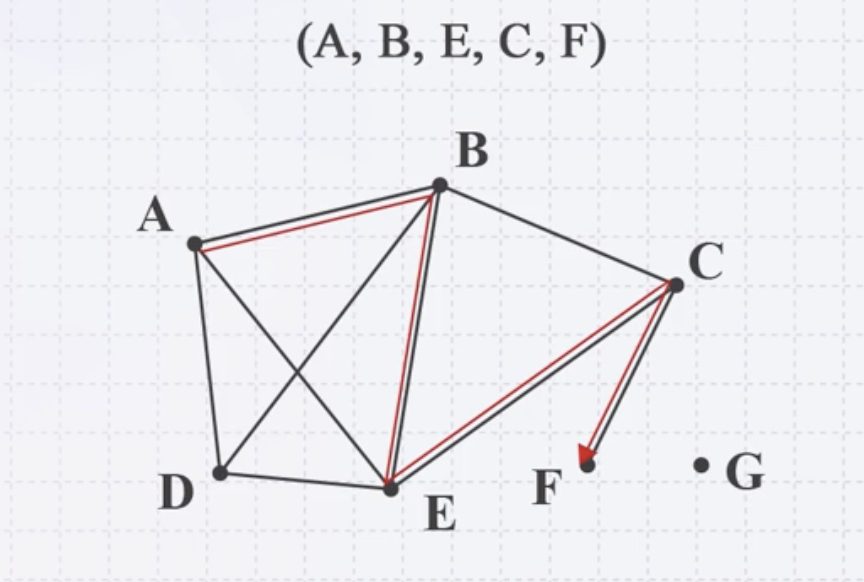A-B-E-C-F로 이어지는 경로의 길이는 4라고 할 수 있다.
- trivial path: 길이가 0인 자기자신에 머무르는 경로
- simple path: 경로의 처음과 마지막을 제외했을 때, 안에 중복이 없는 경로
| O | X |
|---|---|
| A-B-C-A | A-B-C-B-A |
Weighted Graphs 엣지가 단순히 연결성만을 표현하는 것이 아니라 거리와 같은 어떤 값을 표현하는 그래프.
Trees 트리도 그래프의 일종이라고 할 수 있다. 어떤 그래프가 트리가 되기 위해서는
- Connected, 즉 모든 vertex에서 모든 다른 vertex로 가는 경로가 unique하게 존재해야 한다.
- 엣지의 개수가 노드의 개수보다 하나 적다.
- 사이클이 존재하지 않는다.
Directed Graphs 엣지에 방향성이 존재한다.
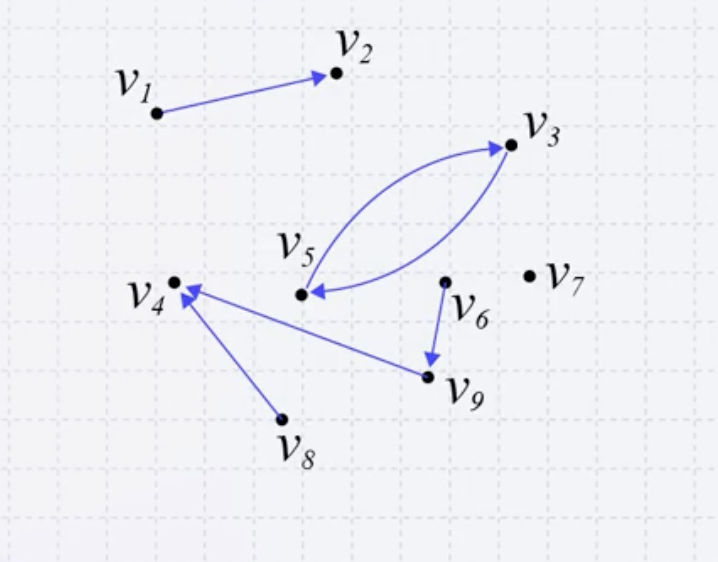
(v1,v2)로 표현되는 엣지는 v1 에서 v2의 방향으로 경로가 존재하는 엣지의 방향성을 갖는다.
- in_degree : 기준 vertex로 들어오는 엣지의 개수
- out_degree : 기준 vertex로부터 출발하는 엣지의 개수
- source : in_degree가 0인 vertex
- sink : out_degree가 0인 vertex
(그래프를 표현하는 방법)
- binary-relation list 엣지들을 나열해놓은 것으로 엣지 개수만큼의 메모리가 필요하다. 어떤 두 vertex 사이가 연결됐는지 확인하기 위해 최대 엣지 개수만큼 프로세싱을 해야 하기 때문에 굉장히 비효율적이다.
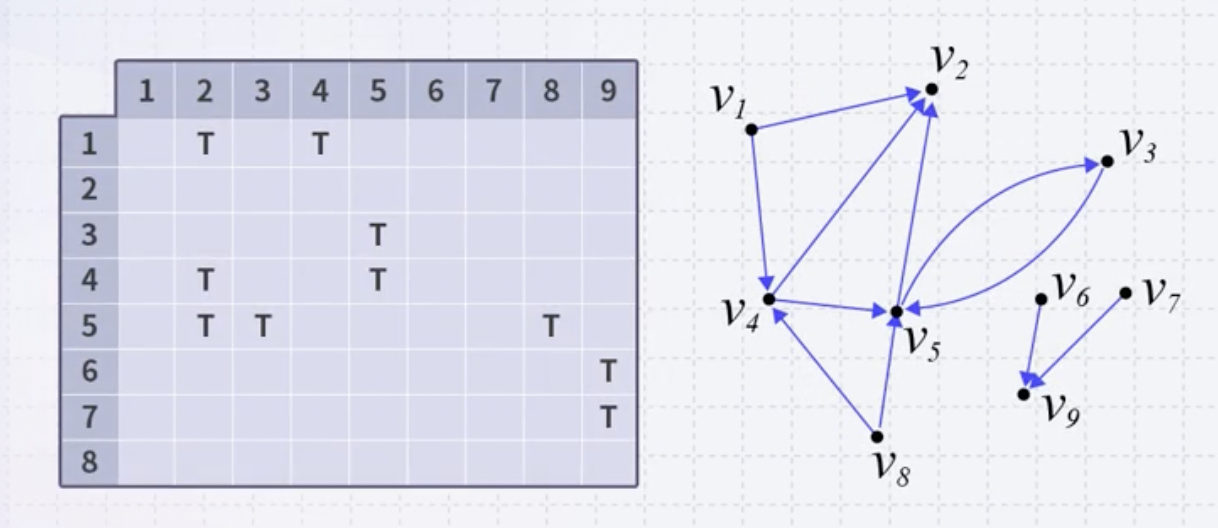
- adjacency matrix 예를 들어, v1에서 v4로 가는 엣지가 잇을 때 2차원 매트릭스 엔트리 (1,4)를 true로 셋팅한다. 이는 v1에서 v4로 가는 엣지가 존재한다는 의미이다. vertex개수가 V라고 했을 때, V제곱 만큼의 메모리가 사용되기 때문에 비교적 메모리를 많이 사용하는 방법이다. v5의 이웃을 구하고 싶다고 할 때, 2차원 매트릭스 상의 다섯번째 줄에서 true인 값만 체크할 수 있다. 따라서, V개 만큼의 작업이 요구된다.
- adjacency list 일반적인 알고리즘에서 가장 많이 사용하는 표현방식. 각 노드들을 기준으로 자신과 연결되어 있는 엣지가 있는 vertex를 리스트로 표현한다. 전체 vertex 수만큼의 linked list가 필요하고 최대 vertex 혹은 엣지 개수만큼의 메모리를 사용한다.