함수의 점근적 분석 (asymptotic analysis)
문제의 크기가 아주 크게 증가했을 때, 우리가 갖고 있는 이 알고리즘은 얼마 만큼의 계산량을 요구하는가를 분석한다. 만약 같은 문제를 푸는 서로 다른 2개의 알고리즘을 갖고 있다고 했을 때, 어떤 알고리즘이 더 좋은 지에 대해 과학적이고 수치적으로 표현할 수 있다.
두 알고리즘을 비교하기 위해 프로그램을 짜서 테스트를 해보는 것이 가장 간단한 방법이다. 실제로 알고리즘 소요시간과 소비 메모리를 측정할 수 있지만 프로그래밍 비용이 비싸고 human error가 발생할 수 있다. 따라서 알고리즘을 수학적으로 분석해 비교해보자는 것이다.
- 하나 이상의 variable과 관련하여 알고리즘을 분석한다.
- 어떤 배열에 몇개의 N개의 요소가 있다. -> N이 variable이 된다.
Linear and Binary Search
Linear Search
배열에서 특정한 값을 찾을 대 앞에서부터 순차적으로 찾는 방법
Binary Search 중간값과 찾고자 하는 값을 비교해 대소관계에 따라 반은 검색 대상에서 제외, 나머지 반에서 검색을 반복 수행하는 방법. 단, 배열이 정렬되어 있을때만 가능하다.
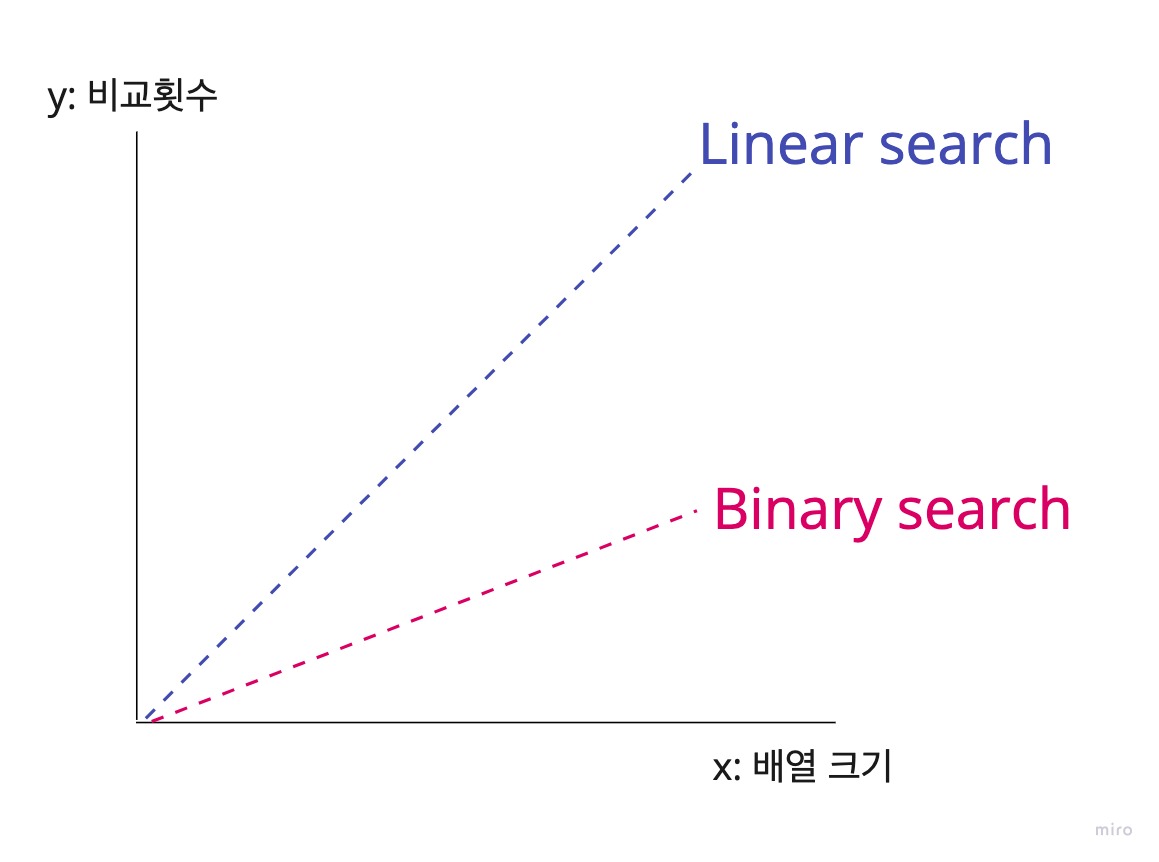
Linear search는 선형적으로 증가하는 반면 Binary search는 x의 값이 증가해도 y의 증가폭은 낮다는 것을 알 수 있다. 즉, Linear search보다 Binary search가 효율적인 알고리즘이라고 할 수 있다.
알고리즘이 주어졌을 때 알고리즘의 성능을 테스트하는 지표로 무엇을 삼을 것인지 선택해야 한다. (위의 알고리즘에서는 ‘비교횟수’가 알고리즘의 계산량을 표현하는 variable이 됐다.) 뿐만 아니라 알고리즘과 자료구조의 관계를 고려해 점근적 분석을 수행해야 하며 기계에서 구동시키는 것과 독립적으로 수학적으로만 이뤄져야 한다.
Weak ordering

첫번째 알고리즘이 f(n)의 복잡도를 갖고 f(n)만큼의 시행횟수를 요구한다. 마찬가지로, 두번째 알고리즘이 g(n)의 복잡도를 갖고 g(n)만큼의 시행횟수를 요구한다. a_k와 b_k가 0이 아니고 f(n)과 g(n)이 모두 n^k 승을 최고차항일 때,
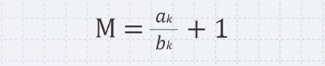
어떤 M이라는 숫자를 설정하면 a_k와 b_k가 어떤 값이 되도 M x g(n)을 f(n)보다 크게 만들 수 있다.
즉, f(n)이 더 커서 g(n)이 더 효율적인 알고리즘이라고 해도 M배 빠른 컴퓨터로 f(n)에 해당하는 알고리즘을 구동시키면 속도차이가 뒤집힐 수 있다. 최고차항 앞의 계수 부분은 더 빠른 컴퓨터로 커버할 수 있지만 최고차항의 승수가 다르면 따라잡을 수 없는 속도 차이가 생긴다.
이를 기반으로 Weak ordering이라는 개념을 도입한다.
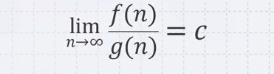
두 함수가 주어졌을 때, 이 둘의 비율인 g(n)분의 f(n)이 n이 무한대로 증가할 때 어떤 constant에 수렴하면 두 알고리즘은 비슷한 복잡도를 가지고 있다고 하고 f~g로 표현한다.
이 비율의 값이 0에 수렴하면 g(n)이 더 큰 것으로 f<g로 표현한다.
n^2과 2n^2은 같은 동일선상에 놓고 대소관계를 구분하지 않기 때문에 weak ordering이라는 표현을 사용하는 것이다.
정리
f(n)과 g(n)이 동일 선상에 있다고 할 때, 더 빠른 컴퓨터를 사용하면 이 둘의 격차를 뒤집을 수 있으며, 반대로 g(n)이 f(n)보다 더 커서 빠른 컴퓨터를 사용해도 이 둘의 대소관계를 뒤집을 수 없을 때 f(n)의 알고리즘이 g(n)의 알고리즘보다 효율적이라고 얘기할 수 있다.
노테이션 (notation)
n이 크게 증가했을 때, 알고리즘의 복잡도가 어떤 양상을 띄는 지 표현할 수 있는 표기법으로 여러 가지가 있다.
세타노테이션 (Θ-Notation)
어떤 함수의 f(n) (시행 횟수, 런타임 등)이 Θg(n)이라는 것은 아래의 조건을 만족한다는 뜻이다.
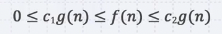
n0보다 큰 모든 n에 대해서 f(n)이 c1g(n)과 c2g(n)사이에 존재한다면 f(n)은 Θ of g(n)이라고 표현할 수 있다.
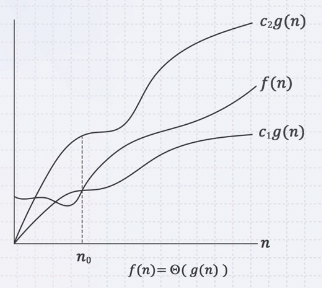
이 때, f(n)은 g(n)과 같은 증가속도를 갖는다 혹은 f(n)은 Θg(n)에 속한다 고 한다.
또한, g(n)은 f(n)의 asymptotically tight bound이다. 즉, n이 점근적으로 커졌을 때 g(n)이 f(n)을 위아래로 가둔다고 해서 점근적 상한과 하한의 교집합이라고 한다.
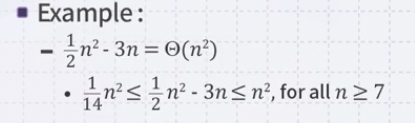
빅오 노테이션 (O-Notation)
세타 노테이션에서 아래쪽을 제외한 위쪽만 취하는 노테이션으로 f(n)이 O of g(n)이라는 것은 f(n)이 0보다 크지만 cg(n)보다는 작다는 것을 의미한다.
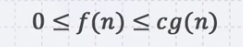
n0보다 큰 모든 n에 대해서 위의 조건을 만족하는 c와 n0가 하나라도 존재하면 f(n)은 O of g(n) 이라고 얘기할 수 있다.
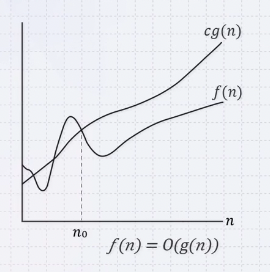
이 때, g(n)을 f(n)의 asymptotically upper bound이다. 또한, f(n)이 Θg(n)이면 O of g(n)이라고 할 수 있다.
알고리즘이 아무리 느려도 이것보다는 빠르다와 같이 최악의 경우에 갖는 러닝 타임을 표현할 때 유용하게 사용할 수 있다.

오메가 노테이션 (Ω-Notation)
빅오 노테이션과 반대로 위쪽을 제외한 아래쪽을 취하는 노테이션으로 f(n)이 Ω of g(n)이라는 것은 f(n)이 cg(n)보다 크다는 것을 의미한다.
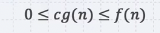
n0보다 큰 모든 n에 대해서 위의 조건을 만족하는 c와 n0가 하나라도 존재하면 f(n)은 Ω of g(n) 이라고 얘기할 수 있다.
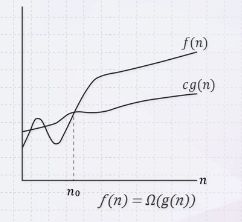
이 때, g(n)을 f(n)의 asymptotically lower bound이다. 또한, f(n)이 Θg(n)이면 Ω of g(n)이라고 할 수 있다.
알고리즘이 아무리 빨라도 이것보다는 느리다와 같이 최선의 경우에 갖는 러닝 타임을 표현할 때 사용할 수 있다.
f(n) = Θg(n) if and only if f(n) = Og(n) and f(n) = Ωg(n)
노테이션의 특성
예시로 세타를 사용했지만 모든 특성은 빅오, 빅오메가 노테이션에도 동일하게 적용된다.
transitivity
f(n) = Θg(n) and g(n) = Θh(n) imply f(n) = Θh(n)
reflexivity
f(n) = Θf(n)
symmetry
f(n) = Θg(n) if and only if g(n) = Θf(n)
transpose symmetry
f(n) = Og(n) if and only if g(n) = Ωf(n)
정리
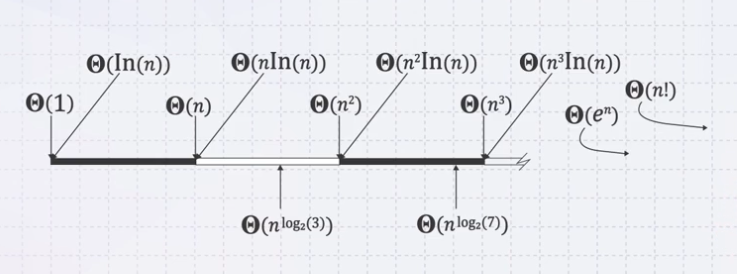
constant가 제일 빠른 알고리즘으로 그림의 왼쪽에 있을수록 효율 적인 알고리즘이라고 얘기할 수 있다.